KOMBİNASYON, KOMBİNASYONUN ÖZELLİKLERİ İLE İLGİLİ KONU ANLATIMLAR (MATEMATİK DERSİ İLE İLGİLİ KONU ANLATIMLAR)
n elemanlı bir kümesin r elemanlı bir alt kümesine n nin r li bir kombinasyonu denir.
Örneğin A = {a, b, c, d} 4 elemanlı bir kümenin üçlü kombinasyonları;
{a, b, c} , {a, b, d}, {a, c, d}, {b, c, d} olmak üzere 4 tanedir. Bunların her biri A nın üçlü bir kombinasyonudur.
n elemanlı bir kümenin r elemanlı kombinasyonlarının sayısı

simgeleri ile gösterilir. Bu sayı ise

olarak da yazılabileceğini görünüz.
n elemanlı r li kombinasyonlarının sayısı için şu dört eşitlik ve özelliği gösterebiliriz.

IV) r sayısı 0 dan başlayarak  den küçük en büyük tam sayıya kadar değiştiğinde
den küçük en büyük tam sayıya kadar değiştiğinde gitgide artan değer alır.
gitgide artan değer alır.

içinde gitgide azalan değerler alır. (r ile n-r değerlerinde ise eşit olmaktadır.)
ÖRNEK:
Herhangi üçü doğrusal olmayan 10 nokta kaç doğru belirtir?
ÇÖZÜM:
10 nun ikili kombinasyonları kadar doğru belirtilir.  = 45
= 45
ÖRNEK :
Herhangi üçü doğrusal olmayan 10 noktayla köşeleri bu noktalar olan kaç üçgen çizilebilir?
ÇÖZÜM :
10 nun üçlü kombinasyonları kadar üçgen çizilebilir.

ÖRNEK :
Üçü bir doğru diğer dördü bir doğru üzerinde olan 7 nokta kaç doğru belirtir?
ÇÖZÜM:

Şekilde görüldüğü gibi 3 nokta bir doğru 4 noktada bir doğru üzerindedir.
Önce 7 noktadan

doğru geçer.
3 noktadan

doğru geçerdi ancak bu 1 doğru üzerindedir.
4 noktadan

doğru geçerdi ama şimdi 1 doğru geçiyor. O halde 21 – 3 + 1 – 6 + 1 = 14 doğru bulunur.
Pratikte d1 doğrusu üzerinde 3 nokta d2 doğrusu üzerinde 4 nokta var.
Bunlardan
3.4 = 12 doğru geçer. d1 ve d2 yi alırsak
12 + 1 + 1 = 14 doğru bulunur.
ÖRNEK :
Bir sınavda 12 soru sorulmuştur. Baştan 3 soruyu herkesin yapması zorunludur. Diğer sorulardan 7 tane seçerek yanıtlaması istenmektedir. sınava giren bir öğrenci bunu kaç değişik şekilde yapabilir?
ÇÖZÜM :
12 –3 = 9 sorudan 7 tane seçecektir.
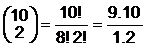
değişik seçenek vardır.
ÖRNEK :
Birbirine paralel 5 doğru ile bunları kesen ve birbirine paralel 6 doğru çiziliyor. Bu doğrular kaç tane değişik paralel kenar oluşturur?
ÇÖZÜM :

Verilen doğrular şekilde olduğu gibi d1, d2, d3, d4, d5 ve a1, a2, a3, a4, a5, a6 olsun. Karşılıklı kenarları olan dörtgenler paralel kenar olduğu için paralellerden ikişer ikişer almanız gerekir. O halde paralel kenar sayısı

ÖRNEK :

ÇÖZÜM :
Yamuk, karşılıklı iki kenarı paralel diğer iki kenarı paralel olmayan dörtgendir. O halde yamuk sayısı,

ÖRNEK :
10 voleybol oyuncusundan belli biri kaptandır. Kaptan daima takımda bulunmak üzere 6 kişilik değişik kaç voleybol takımı kurulabilir?
ÇÖZÜM :
Biri her takımda bulunacağı için 9 oyuncudan 5 ini seçmek gerekir. O halde

ÖRNEK :
9 kişilik bir gruptan 5’i A, 4’ü B kentine kaç değişik biçimde gider?
ÇÖZÜM:
9 kişiden 5’i A kentine gider geriye kalan 4’ü B ye gider. O halde yalnız A kentine giden-lerin sayısını bulmak yeterlidir.

ÖRNEK :
10 kişilik bir gruptan 5’i A, 3’ü B ve 2’si C kentine kaç değişik biçimde gider?
ÇÖZÜM :

ÖRNEK :
C(n,2) = 45 ise n kaçtır?
(C(n,2) , n elemanlı ikili kombinasyonlarının sayısıdır.)
ÇÖZÜM:

ÖRNEK :
bir torbada 5 kırmızı, 12 Beyaz bilye vardır. Bu torbadaki bilyelerle 1 kırmızı 3 beyaz olmak üzere kaç değişik grup bilye elde edilir?
ÇÖZÜM :

ÖRNEK :
Bir sandıkta bulunan 12 ampulden 4 ü bozuktur. Bu sandıktan 1 i bozuk 3 ü sağlam olmak üzere kaç değişik grup oluşturulabilir?
ÇÖZÜM :
4 ü bozuksa 8 i sağlamdır. O halde,

Olasılık Konu Anlatımı
A. TANIM
Olasılık, sonucu kesin olmayan olaylarla ilgilenir. Bir zar atıldığında üst yüze gelen noktaların sayısının ne olacağı gibi şans oyunlarıyla ilgilenen olasılık teorisi günümüzde sosyal olaylar ve bilimsel çalışmalarda da kullanılmaktadır.
B. OLASILIK TERİMLERİ
Bir madeni para havaya atıldığında yazı mı ya da tura mı geleceğini (v.b) tesbit etme işlemine deney denir.
Bir deneyin her bir görüntüsüne (çıktısına) sonuç denir.
Bir deneyin bütün sonuçlarını eleman kabul eden kümeye örnek uzay denir.
Bir örnek uzayın her bir alt kümesine olay denir.
Örnek uzayın alt kümelerinden olan boş kümeye imkansız (olanaksız) olay denir.
Örnek uzayın bütün elemanlarını içeren alt kümesine kesin olay denir.
A ve B, E örnek uzayına ait iki olay olsun.
A Ç B = Æ
ise, A ve B olayına ayrık olay denir.
C. BİR OLAYIN OLASILIĞI
Örnek Uzayı “E”, bir olayı “A” ve A olayının olasılığını da O(A) ile gösterirsek;
ile gösterilir.
-
Bir olayın olasılığı 0 ile 1 arasındadır.
0 £ O(A) £ 1 dir.
-
O(A) = 0 ise A olayının gerçekleşmesi mümkün değil demektir. (İmkansız olayın olasılığı 0 dır.)
-
O(A) = 1 ise A olayı kesinlikle gerçeleşecek demektir. (Kesin olayın olasılığı 1 dir.)
-
O(A), A olayının olma olasılığı,
O(Aı), A olayının olmama olasılığı olmak üzere,
O(A) + O(Aı) = 1, yani bir olay ya olur veya olmaz demektir. Bu ifadeyi
O(A) = 1 – O(Aı) şeklinde de düşünebiliriz.
|
-
A Ì B ise O(A) £ O(B) dir.
-
n, paranın atılma sayısını veya para sayısını göstermek üzere, örnek uzay 2n dir.
-
n, zarın atılma sayısını veya zar sayısını göstermek üzere, örnek uzay 6n dir.
|
D. AYRIK İKİ OLAYIN BİRLEŞİMİNİN (A VEYA B OLAYININ)OLASILIĞI
A Ç B = Æ ise,
O(A È B) = O(A) + O(B) dir.
E. AYRIK OLMAYAN İKİ OLAYIN BİRLEŞİMİNİN (A VEYA B OLAYININ)
OLASILIĞI
O(A È B) = O(A) + O(B) – O(A Ç B) dir.
F. BAĞIMSIZ OLAYLAR
Bir olayın elde edilmesi, diğer olayın elde edilmesini etkilemiyorsa bu iki olaya bağımsız olaylar denir.
A ve B bağımsız iki olay olsun. A nın ve B nin gerçekleşme olasılığı :
O(A Ç B) = O(A) . O(B) dir
(ALINTIDIR)
